はじめてのGrasshopper変換入門：MoveやRotateのしくみを解説

こんにちは、篠原です。

Grasshopperでモデリングを行う際、「動かす」「回す」「サイズを変える」といった操作は頻繁に使われます。MoveやRotateといったコンポーネントをつなぐことは、多くのユーザーにとって日常的な作業です。

このような変形操作の背後には、RhinoおよびGrasshopperの内部で共通して使われている「Xform（Transform）」という仕組みがあります。本記事では、Grasshopperユーザーを対象に、アフィン変換とXformの基本的な考え方を紹介します。

Grasshopperでは、ジオメトリを動かしたり回転させたりするときに、専用の変換コンポーネントを使用します。以下は代表的なコンポーネントです。

これらのコンポーネントでは、操作の内容に応じた「変換情報（Xform）」が内部的に生成され、それが指定されたジオメトリに適用されます。ユーザーはこの変換情報を意識せずとも、接続とパラメータ指定によってジオメトリを自在に変形できます。

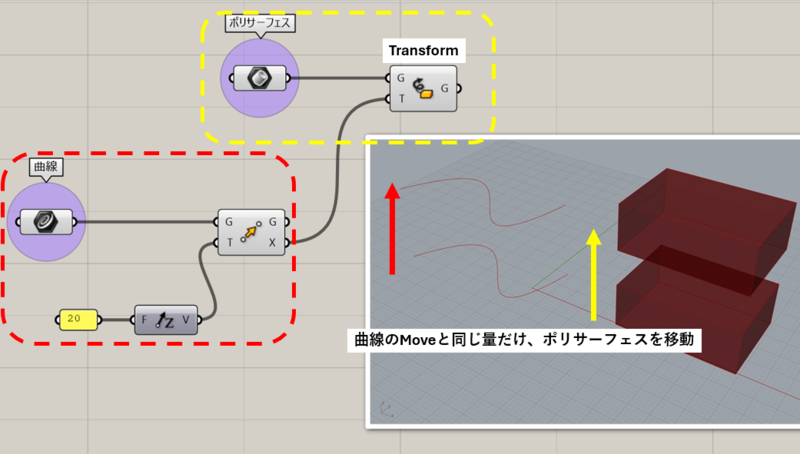
また、Transformコンポーネントは、MoveやRotateなどで作成したXformを他のジオメトリに再利用するために使われます。

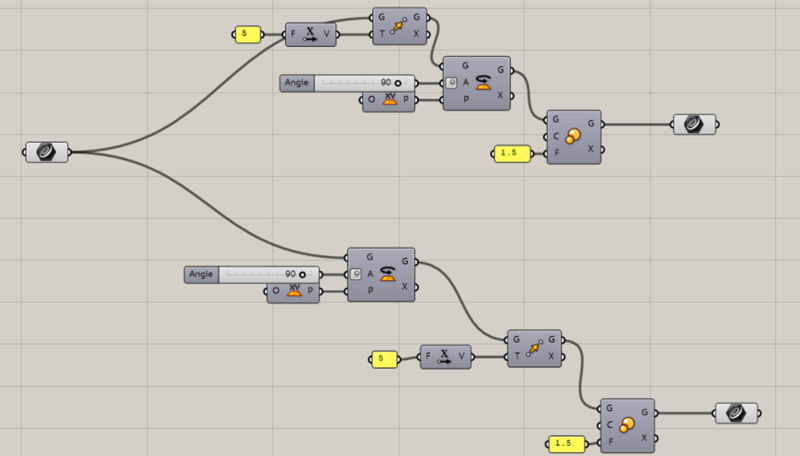
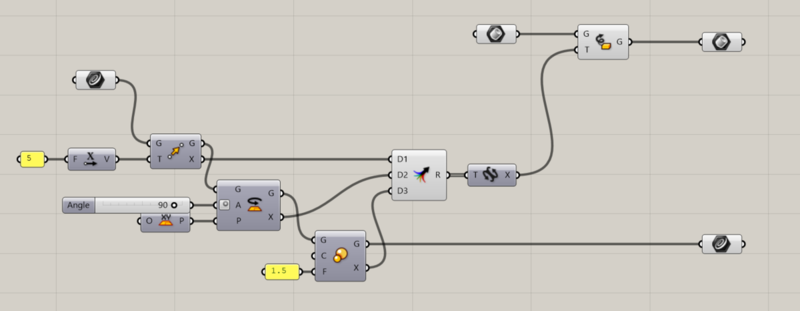
Grasshopperでは、複数の変換を連続して適用することも可能です。以下のように段階的に変形させることができます。

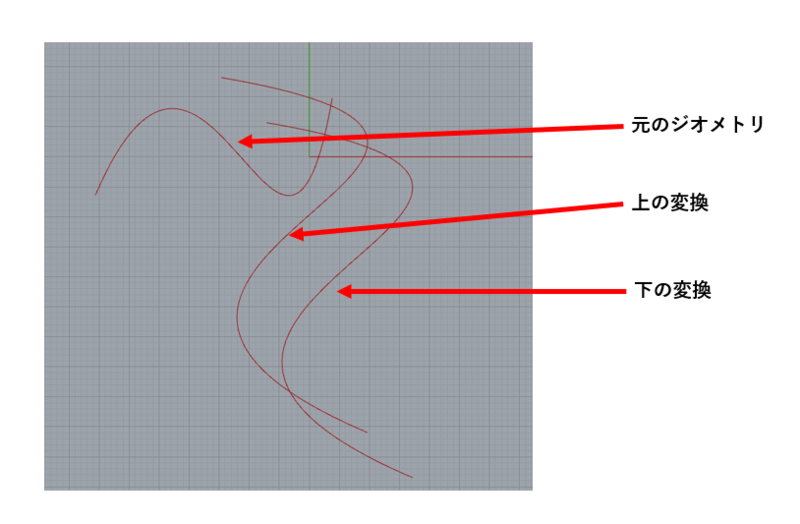
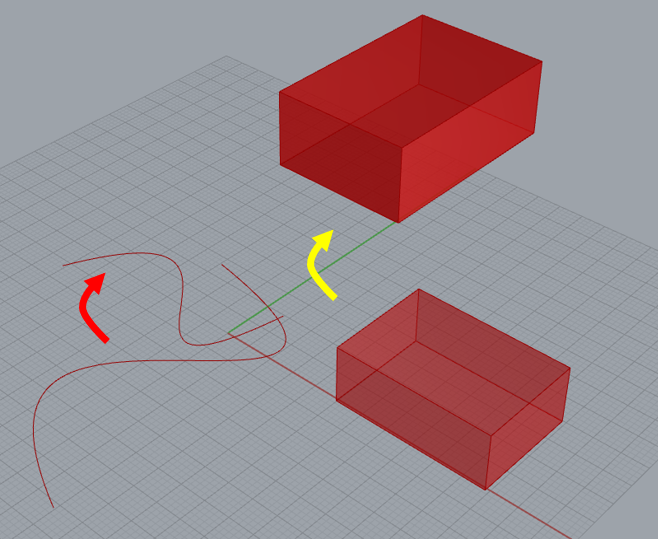
このような操作は、それぞれの変換コンポーネントを直列につなげることで実現します。ただし、変換の順序には注意が必要です。同じ操作でも順序が異なれば結果も変わります。たとえば、回転してから移動するのと、移動してから回転するのとでは最終位置が異なります。

ここまで紹介したGrasshopperの変換コンポーネントのほとんどは、アフィン変換（Affine Transformation）と呼ばれる数学的な枠組みに基づいています。

アフィン変換とは、オブジェクトの幾何的な関係を保ったまま、次のような操作を行う変換のことです。

アフィン変換の特徴は、変換後も直線が直線のまま保たれること、平行性が保たれることです。ジオメトリが歪んだり、ねじれたりすることはありません。

Grasshopperでは、ユーザーがこれらをコンポーネントとして接続して操作しますが、内部的にはすべて行列の計算として処理されています。

RhinoやGrasshopperでは、こうしたアフィン変換を統一的に扱うためにTransform（Xform）という仕組みを使っています。Transformは4×4の変換行列で構成されており、位置・回転・拡大縮小などの情報をすべて一つの形式で保持できます。

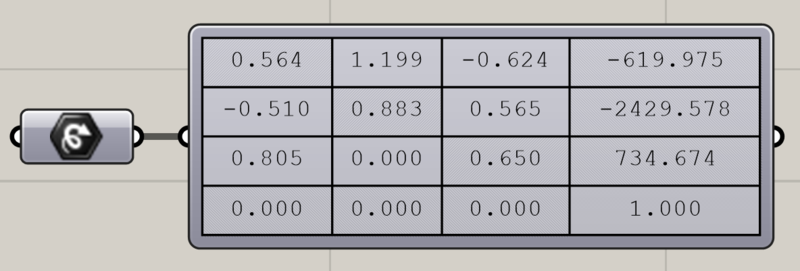
GrasshopperのTransformコンポーネントでは、MoveやRotateの出力を組み合わせることで、複数の変換を一括して適用できます。これにより、複雑な配置やパターン生成が効率的に行えるようになります。

Rhinoでは、Block機能を使って同じジオメトリを複数の場所にインスタンス化できます。Blockの各インスタンスは、共通のブロック定義と、それぞれ異なるXform（変換情報）で構成されています。

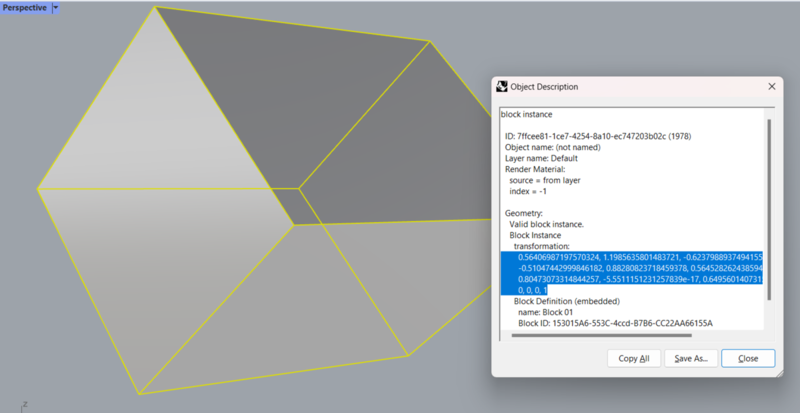
つまり、同じオブジェクトが異なる位置・角度・スケールで表示されていても、中身は一つの定義で共通化され、表示上の違いはXformによって作られています。

GrasshopperからBlockを操作したい場合は、elefrontプラグインを利用することで、Blockの挿入や変換を制御できます。これも、Xformを使った操作の一種です。

Grasshopperを使ってモデリングする際、変換コンポーネントは非常に基本的な存在です。しかし、それらがどのような仕組みに基づいて動いているかを理解すると、より柔軟で構造的な操作が可能になります。

Xformの考え方を理解しておくことで、複雑な変形やパターンの作成、Blockの再利用など、設計の幅を広げることができます。

今後Grasshopperでのモデリングを進めていく中で、「この操作はどんな変換に基づいているのか？」と考える習慣をつけると、より論理的で安定した設計ができるようになります。

vicc blog