前回(#2)の記事から引き続き「曲線と曲面の連続性」に焦点を当てて説明していきます。今回は前回扱った曲線の連続性を発展させ、曲面の連続性について説明したいと思います。
目次
・G0連続
・G1連続
・G2連続
・曲面の連続性と光の反射の関係
・生産設計の視点から
G0連続
2枚の曲面が共通の境界曲線で接続しているとき、それらの曲面はG0連続であるといえます(図1)。
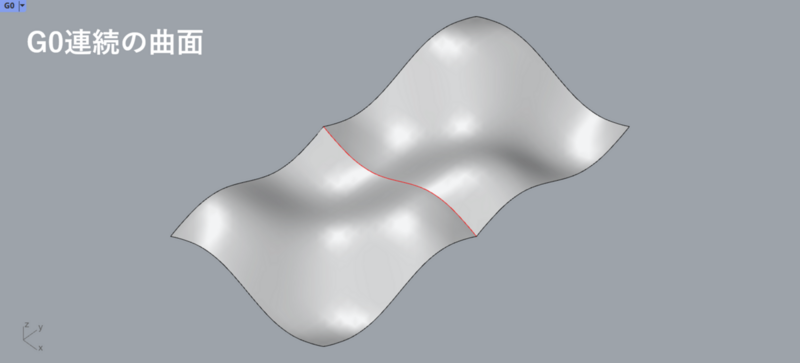
曲線のG0連続では境界は点でしたが、曲面では境界は曲線(直線を含む)となります。折紙で言うと谷折りや山折りの部分はG0連続となります。
G1連続
曲面S上のある点pから発する全ての接ベクトルによって定義される1枚の平面を、点pにおける接平面(tangent plane)と呼びます。接平面は点pにおいて曲面Sに接し、点pにおける曲面Sの法線nと直交します(図2)。
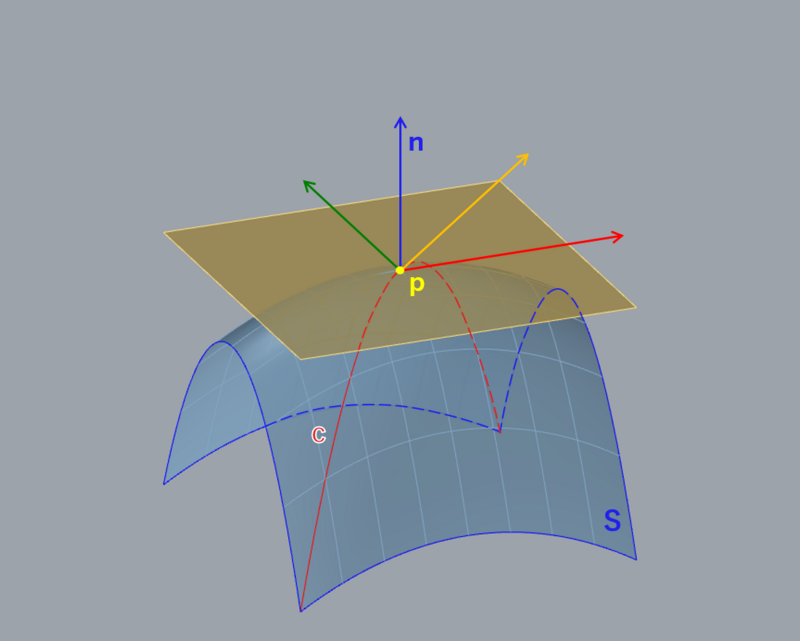
G0連続に加え、共通の境界曲線上の全ての点において接平面が一致しているとき、2枚の曲面はG1連続となります(図3)。
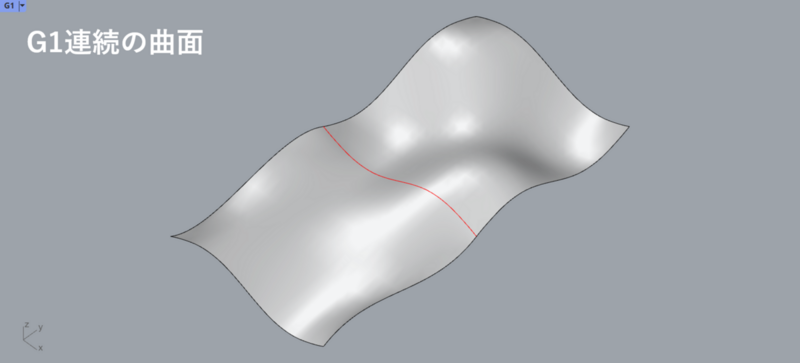
曲線では接線の一致がG1連続の条件でしたが、曲面では接平面の一致が条件となります。
G0連続の曲面では境界曲線を境に接平面の傾きが不連続となりますが、G1連続の曲面では連続となります(図4,5)。


G2連続
曲面S上のある点pにおいて法線nを通る平面Rで曲面Sを切断した断面曲線をcとしたとき、曲線cの点pにおける曲率を法曲率(normal curvature)と呼びます。平面Rを法線nを軸に回転させることで点pにおける法曲率は無数に存在し、その中の最大値と最小値が前々回(#1)で触れた主曲率となります(図6)。
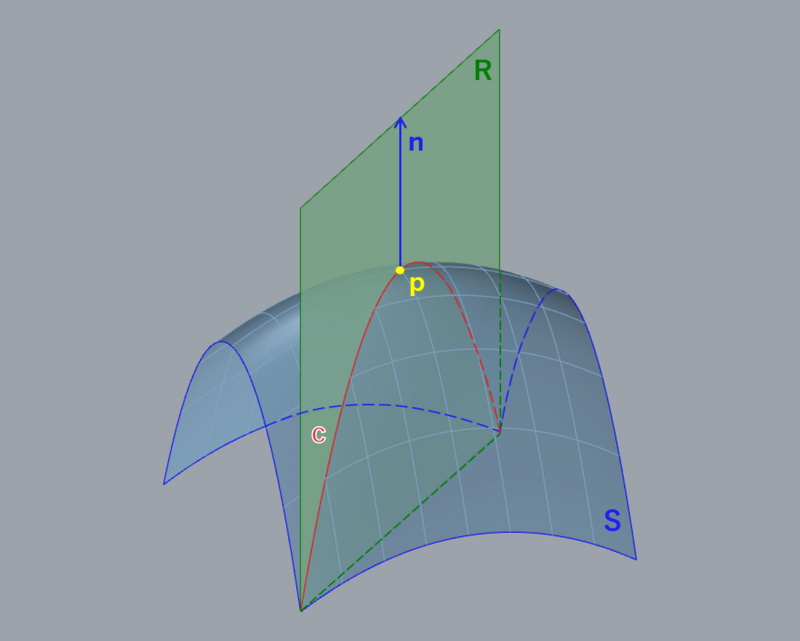
G1連続に加え、共通の境界曲線上の全ての点における全ての接ベクトル方向において法曲率が一致しているとき、2枚の曲面はG2連続となります(図7)。

曲線では曲率の一致がG2連続の条件でしたが、曲面では法曲率の一致が条件となります。
G1連続の曲面では境界曲線を境に法曲率の値が不連続(グラフに段差がある)となりますが、G2連続の曲面では連続となります(図8,9)。


曲面の連続性と光の反射の関係
実は曲面の連続性は、光の反射の仕方と関係があります。
原理の説明を省き結論を言うと、「反射する模様(曲線)の連続性=曲面の連続性-1」という関係性が成り立ちます。
G0連続の曲面上では境界曲線における反射模様の連続性は位置不連続となります(図10)。
明らかに境界曲線で反射模様が分断しています。

G1連続の曲面上では境界曲線における反射模様の連続性はG0連続(位置連続)となります(図11)。
一見なめらかに反射模様が繋がっているように見えますがよく見ると境界曲線で折れています。

G2連続の曲面上では境界曲線における反射模様の連続性はG1連続(接線連続)となります(図12)。
境界曲線で反射模様に折れがなくなめらかに繋がっています。

以上のことから、鏡面の金属やガラスなどの反射性のある材料で曲面形状をつくるときは、より曲面の連続性が大切であることが分かるのではないでしょうか。
生産設計の視点から
ここまで理想的な曲面の連続性についてその幾何学的な定義を説明してきましたが、実際の建築物では十分になめらかな連続性をもった曲面形状を実現することはコスト的に難しいとされています。
全体として連続的でなめらかな複曲面のようにみえる建築物も、単曲面や平面で近似した単位部材による離散的な曲面で構成されていることが多いのではないでしょうか。
この件に関しては前々回(#1)の記事で触れたのでぜひご参照ください。
参考文献
[1] 宮岡礼子 . 曲線と曲面の現代幾何学-入門から発展へ . 岩波書店 . 2019
[2] Helmut Pottmann , Andreas Asperl , Michael Hofer , Axel Kilian . Architectural Geometry . Bentley Institute Press . 2007
[3] Erich Hartmann . Geometry and Algorithms for Computer Aided Design . Department of Mathematics, Darmstadt University of Technology . 2003
[4] Joseph Pegna , Franz-Erich Wolter . Geometrical Criteria to Guarantee Curvature Continuity of Blend Surfaces . Journal of Mechanical Design . 1992 , Vol.114 , p.201-210 .