こんにちは、新入社員の篠原と申します。
皆さんは「Brep」という言葉を知っていますか?「Boundary Representation」の略称で、「ビーレップ」や「ブレップ」と読み、直訳すると「境界表現」ですね。
これは、我々が3DCADでモデリングしたい形状を、その境界(表面)だけで表現するという考え方です。RhinocerosユーザーだとPolysurfaceという呼び名のほうが聞きなじみがあるかもしれません。
3D CADの扱いにはさまざまな専門知識が必要ですが、モデリング一般において、特に幾何学を中心とした数学の知識は非常に役に立ちます。次の記事では、3D CADの数理的な扱いについて網羅的にかかれています。
これまでvicc blogでは「建築実務者なら~」シリーズで、曲面の曲がり具合について書いてきました。
この内容は曲面形状を実現させるにあたって非常に重要な考え方です。
ヴィックでは、すこしでも安く、良い曲面にする、合理的な製造や施工に向けて、この考えに基づいて設計サポートをしています。
そして今回は、「そうは言っても現時点で製造のことまで考えきれないから、まずは泥臭くモデリングしたい!」という建築実務者の方々に向けて、関係者間で形状データをこねくりまわしても後々困らないようなモデリングに役立つ、Brepのしくみについてお伝えしようと思います。
立体的な曲面を、平面的な紙の上にかいてみる
本題に入る前に、「ケーニヒスベルクの七つの橋問題」について説明します。

数学者ガウスは、図1の7つの橋を一回ずつ渡って元の位置に戻るルートはないと証明しました。
証明では、図2のように場所の関係性のモデルを立てて論じました。このモデルは「グラフ」と呼ばれ、特に、青い点は「頂点(vertex)」と、破線は「辺(edge)」と呼ばれます。
これは「グラフ理論」という数学で、Googleマップなどのための技術に応用されています。

ガウスのモデル化と似た方法で、さまざまなものをグラフにモデル化できます。
図3は、名古屋駅から各地の駅までの所要時間を、それらを結ぶ辺の長さとしてモデル化された日本地図で、グラフィックデザイナーの杉浦康平氏によって制作されました。
このように、我々がよく知る地球儀上の日本列島の形状を、交通というルールを使って変形することができます。

杉浦ら. 時間のヒダ、空間のシワ…[時間地図]の試み: 杉浦康平のダイアグラム・コレクション. 鹿島出版会, 2014/9/26
NURBSの構造を確認する
Brepの境界たらしめるものは、一般的にNURBS(Non-Uniform Rational B-Splines)と呼ばれるルールでモデル化された曲面形状です。NURBS曲面は以下の式によって表現されます。
複雑な式ですが、今回は左辺のS(u,v)に着目します。これは、曲面上の点を表しており、この点の無限個の集合が曲面になります。
つまり、NURBS曲面のルールは点の集まり方であり、点はuとvの二つの実数の組み合わせなので、2次元実数空間(平面)があればS(u,v)は実現します。
この2次元実数空間は、どのNURBS曲面モデルにも共通なので、建築Aと建築Bの屋根をNURBS曲面で表現したRoof_A(u,v)とRoof_B(u,v)もまた同じ2次元空間をもち、これを介してRoof_AをRoof_Bに変形することができます。
では、巻物を広げるように、曲面を平面に広げてみましょう。
図4は3D CADで作った図で、右側の平面的な正方形は、左側の立体的な曲面から、曲面を表現するNURBSのルールを使って変形されました。
こうした操作は、コーヒーカップとドーナツが同じだとする観点と同じで、NURBS曲面などのいくつかの曲面を平面に広げ、紙の上にかくことができます。

Brepの構造を確認する
紙にかかれた日本地図は、交通のルールを当てはめて別の紙にかき直すことができます。そして、NURBS曲面は2次元の情報を持っているので、その形は四角形(紙)をゆがめた形になり、NURBS曲面の上にかいたグラフを紙の上にかき直すことができます。
図5はBrepの数学的な構造のダイアグラムで、ここにグラフ理論の考え方を当てはめることができます。
3D SpaceにあるSurfaceは、2D Parameter Spaceにある辺(edge)の情報でTrimされます。EDGEとTRIM、LOOPは、とりあえず辺だと解釈してください。これらの辺はNURBS曲面の上にかかれたグラフです。
特に、辺で囲まれた領域は面(face)と呼ばれ、また面は辺を介して隣接することができます。NURBS曲面は四角形に制限されますが、NURBS曲面を切り貼りして作られたBrepはさまざまな曲面を表現できます。
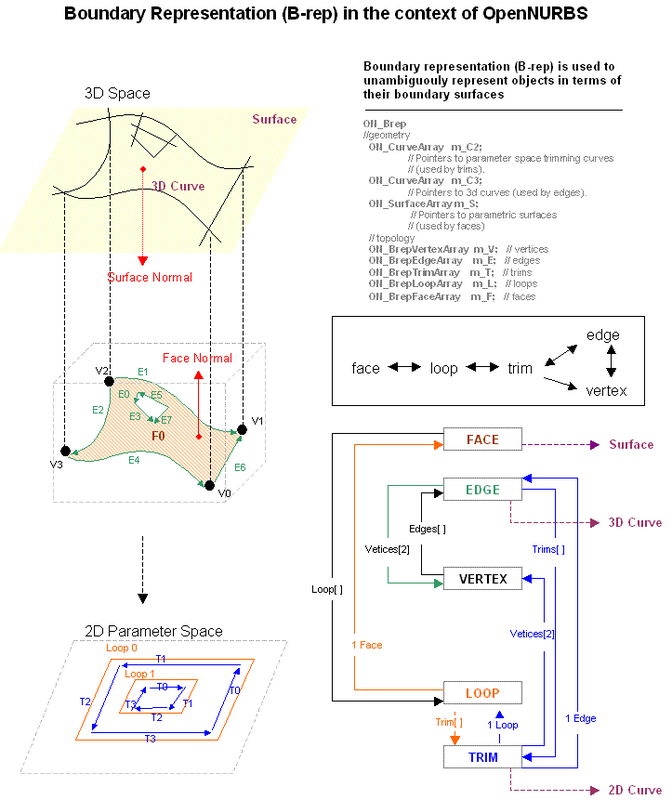
[引用元: https://developer.rhino3d.com/guides/cpp/brep-data-structure/]
図6は、クロスキャップと呼ばれる曲面形状をBrepでモデリングしようとしたもので、これはメビウスの輪やクラインの壺などの仲間です。図中の黒い線はモデリングの過程で生じた辺で、隣接しあう面の集まりで図形全体を構成しています。
これに対して、Brepのグラフを使って数学的な分析が可能です。例えば、図5のFace Normalが存在するという条件により、実は、これは厳密にはクロスキャップではないと結論づけられます。このこともいずれブログに書いてみたいところですが、「Rhinoでクロスキャップをモデリングしました!」という話があれば、それをいったん疑って良さそうだという判断を、3Dモデルを確認する前に可能です。

おわりに
今回は、曲面を紙の上にかくことについて確認するところから、Brepの数学的な構造について確認しました。
この数学的な知識によって丁寧に作られたモデルが、それを受け取るエンジニアを困らせることはほとんどないはずで、そのデザインの建築の施工性を検討する期間は短縮されて実現可能性は高まると思います。
ヴィックでは、さまざまな3Dモデルを実現させるために設計サポートをしています。何か困っていることがあれば、ぜひ一度お問い合わせください。